Praktická elektronika/Spektrum signálu

Zatím jsme se zabývali jen s harmonickým signálem (to je elektrické napětí/proud, který má sinusový průběh v čase). Často se ale setkáme s i s jinými, nesinusovými průběhy. Ukážeme si, že je jde výhodně vyjádřit jako součet sinusových průběhů.

Grafu, který to znázorňuje, se říká spektrum a samotná operace se označuje jako Fourierova transformace.

Spektrum sinusové vlny

Vezměme jednoduchou sinusovou vlnu s danou amplitudou (výchylkou) frekvencí = f₀. Její průběh je:

$U(t)=sin(2\pi \cdot f_0\cdot t)$

Pro takovou vlnu pak vypadá spektrum takto:

Spektrum složeného signálu

Nyní vezměme signál, který je součtem dvou sinusovek o různé frekvenci:

$U(t)=sin(2\pi \cdot f_0\cdot t)+\frac{sin(2\pi \cdot 6f_0\cdot t)}{4}$

Když je signál tvořen součtem více vln, uvidíme je v jeho spektru:

Rozložit signál na jednotlivé sinusovky je někdy velmi užitečné. Můžeme tak spočítat, jaký proud poteče [[../Filtry a jejich přenos/|lineárním obvodem]] pro každou frekvenci zvlášť a pak spočítané proudy prostě sečíst.

Obdélníkový signál

Když budeme sčítat donekonečna sinusové vlny podle vzorce:

$U(t)=\frac{sin(2\pi \cdot f_0\cdot t)}{1}+\frac{sin(2\pi \cdot 3f_0\cdot t)}{3}+\frac{sin(2\pi \cdot 5f_0\cdot t)}{5}+\frac{sin(2\pi \cdot 7f_0\cdot t)}{7}+\frac{sin(2\pi \cdot 9f_0\cdot t)}{9}+\frac{sin(2\pi \cdot 11f_0\cdot t)}{11}+\cdots$,

bude signál stále hranatější a nakonec získá obdélníkový tvar:

Proto obsahuje spektrum obdélníkového signálu nekonečné množství vyšších harmonických:

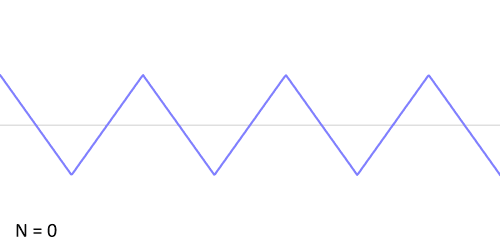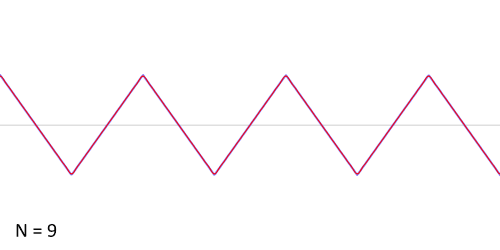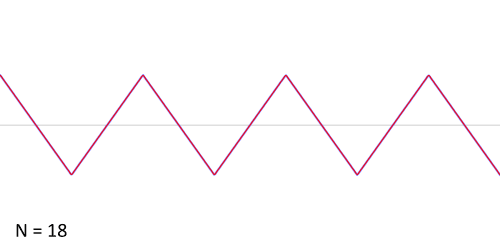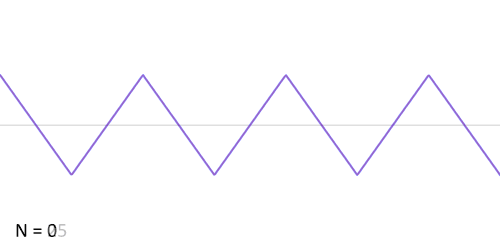
Trojúhelníkový signál

Podle jiného předpisu můžeme vytvořit trojúhelníkový signál:

$U(t)=\frac{sin(2\pi \cdot f_0\cdot t)}{1^2}-\frac{sin(2\pi \cdot 3f_0\cdot t)}{3^2}+\frac{sin(2\pi \cdot 5f_0\cdot t)}{5^2}-\frac{sin(2\pi \cdot 7f_0\cdot t)}{7^2}+\frac{sin(2\pi \cdot 9f_0\cdot t)}{9^2}-\frac{sin(2\pi \cdot 11f_0\cdot t)}{11^2}+\cdots$,

Všimněme si, že se ideálnímu tvaru přiblíží mnohem rychleji než obdélníkový signál:

Spektrum průběhů, které podobně jako trojúhelníkový neobsahují skoky, obsahuje výrazně slabší vyšší harmonické.

Spektrum šumu

Sluneční světlo je krátkovlnné elektromagnetické vlnění, které má náhodný, šumový průběh. Proto v jeho spektru najdeme (skoro) všechny frekvence.

Průběh šumu se nikde neopakuje a najdeme v něm spojité spektrum:

Podle tvaru spektra se rozlišuje řada různých druhů šumů (liší se i zvukem!).

Ostatní průběhy

Fourierovu transformaci lze použít i na obecné průběhy (třeba tóny hudebních nástrojů nebo lidský hlas).

Nejen to, lze jím vyjádřit i průběhy neperiodické (tedy neopakující se v čase) - stačí do spektra zahrnout i velmi nízké frekvence.

Výborný applet na vyzkoušení je na stránkách http://www.falstad.com/fourier/.